Innehåll

Att förstå den matematiska processen som är involverad i att beräkna volymen på en trapets går genom hjärtat av geometrin för konceptuell och praktisk vetenskaplig konstruktion. Texten nedan är ett steg-för-steg-förfarande för att först förstå de grundläggande principerna som följer variablerna i den väsentliga formulerade ekvationen och sedan använda den för att lösa problem med trapezformiga figurer.
Steg 1
Förstå att byggandet av praktiska projekt, såsom bostads- eller kommersiella byggnader, markarbeten som slambäddar och hushållsrör och andra anläggningar, involverar nödvändig kunskap om volymen av flytande ämnen inom stängda platta figurer, vilket gör det möjligt för eleven att förståelse för behovet av att beräkna volymen. Noggrann mätning av befintliga dimensioner leder till en exakt volymberäkning.
På ett praktiskt sätt är det bra att hitta trapezider som tvärsnitt av lerväggar i det geografiska bassängen när man definierar en trapets. Om två sidor av en fyrsidig figur är parallella, men inte lika stora, och de andra två sidorna inte är parallella, kallas den figuren en trapets.
Så om du har en siffra som är 22,86 m lång, med en frontdimension på 17,37 m bred och 10,66 m hög, och som har en botten på 21,94 m bred och 3,65 m i höjd, att beräkna volymen skulle vara att följa följande:
Formen kan ses som en 17,37 x 22,86 rektangel på framsidan, sammanfogad med 21,94 x 3,65 plan längst ner, på ett avstånd av 22,86 m.
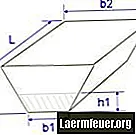
Formeln för att beräkna volymen på detta sätt, som kan ritas som en bagageutrymme med en rektangulär topp och botten istället för fram och bak, kan uttryckas som V = [a1b1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3, där variablerna kan beskrivas med a1 = 17,37; b1 = 10,66; a2 = 21,94; b2 = 3,65; h = 22,86: V = [alb1 + a2b2 + (a1b2 + a2b1) / 2] * h / 3 V = [17,3710,66 + 21,943,65 + (17,373,65 + 21,9410,66) / 2] * 22,86 / 3 V = [265,60 + (63,54 + 234,11) / 2] * 7,62 V = [265,60 + (297,66) / 2] 7,62 V = [414,44] 7,62 V = 3,158,03 m3
Steg 2
Efter formatet skiljer sig den dynamiska volymen för en trapezoid från den för den statiska modellen eftersom en statisk trapezoid är geometriskt en figur med två dimensioner. Området som ska beräknas kan bara vara det för en trapetsformad i två dimensioner på papper. Därför är en alternativ version av formeln med den genomsnittliga bredden och längden: V = [a1b1 + a2b2 + 4 ((a1 + a2) / 2 * (b1 + b2) / 2)] * h / 6 Rektangeln har sidor som är medelvärdet av sidorna på de övre och nedre rektanglarna.
Steg 3
Som i den dynamiska tillämpningen av steg 2 kan volymen på en trapetsformad konstruktion, såsom en pool eller en sluten cylinder, beräknas som liter per meter av en specifik höjd. Det betyder att volymen på en full behållare dividerat med höjden ger sin egen anledning - använd formeln (med mått i m) för att få kubikmeter.
För alla behållare som inte är cylindriska, kommer förhållandet att variera med djup, om studenten vill. Och man kan tro att detta innebär att behållaren skulle fyllas delvis och att volymen skulle bestämmas på olika nivåer. Det vill säga volym är en funktion av höjd.
Steg 4
Går vi lite längre, när bredden i riktningen 'a' ändras linjärt från a1 till a2, a = a1 + (a2-al) k = (1-k) a1 + ka2; enheter kh stiger från botten (där k sträcker sig från 0 till 1); på samma sätt, b = b1 + (b2-bl) k = (1-k) bl + kb2; volymen av det fasta ämnet med höjd kh, bas a1 av b1 och topp a av b är V (k) = [a1b1 + ab + a1b / 2 + ab1 / 2] * kh / 3.
Om vi använder den faktiska vätskenivån istället för k-förhållandet kan vi ersätta k = L / h och vi får V (L) = [(3h ^ 2-3Lh + L ^ 2) a1b1 + L ^ 2a2b2 + (3Lh-2L ^ 2) (alb2 + a2b1) / 2] * L / (3h ^ 2). Detta ger oss volym som en funktion av djupet.
Steg 5
Att beräkna volymen hos en trapezoid på rätt sätt innebär förmågan att tolka om den trapetsformiga figuren är tvådimensionell eller tredimensionell. Den dynamiska övningen av den trapetsformade tolkningstekniska aspekten kretsar kring huruvida den trapetsformiga figuren är något som helt enkelt är designad eller konstruerad, oavsett om den innehåller en volym eller bara är en skiss på papper.